Analyse der derzeitigen Situation
Die momentane Situation auf dem Reifenmarkt ist durch ein – aus Perspektive der Anbieter – optimales friedliches Nebeneinander gekennzeichnet. Besser könnte die Lage gar nicht sein als in diesem stillschweigenden Kartell. Beide Anbieter zusammen produzieren bei der durch Tabelle 1 gegebenen Preis-Absatz-Situation und den aus Tabelle 2 erkennbaren Grenzkosten die Monopolmenge. Sie befolgen die Angebotsregel im Monopol "Grenzumsatz gleich Grenzkosten".
Kartell- oder Monopollösung
Diese Situation ist dargestellt in Abbildung 1. Die Preis-Absatz-Funktion PAF gibt die Information aus Tabelle 1 wieder. Sie lautet
$$ x = 5.000 - 20\cdot p \space \space \space \Leftrightarrow\space \space \space p = 250 - 0,05\cdot x \tag{1} $$wobei $x$ die Anzahl der Reifen in Tsd. und $p$ den Reifenpreis bezeichnet.
Die Kostenfunktion kann wegen der Annahme konstanter Stückkosten angegeben werden als
$$ K = 150x \tag{2}$$Mit der PAF folgt für den Umsatz
$$ U = px = 250x - 0,05x^2 \tag{3}$$Über die Regel Grenzumsatz ($ U'= 250 - 0,1x $) gleich Grenzkosten ($ K' = 150$) berechnet man das optimale monopolistische Angebot zu 1.000 $x$, d.h. eine Million Reifen, und den gewinnmaximierenden Preis zu 200 Euro. Der Umsatz beträgt 200 Mio. Euro, so dass sich bei Kosten von insgesamt 150 Mio. Euro die beiden heimlichen Kartellisten den Profit in Höhe von 50 Mio. Euro teilen.
Cournotsche Duopollösung
Welche Menge und welcher Preis hätten sich eingestellt, wenn die beiden Monopolisten in einen Mengenwettbewerb à la Cournot eingetreten wären? Die Cournotsche Verhaltenshypothese lautet (etwas unrealistisch), dass der Duopolist davon ausgeht, dass der Konkurrent mit seiner Produktion nicht auf eigene Produktionsentscheidungen reagieren wird. Wenn sich beide Duopolisten spiegelbildlich so verhalten, genügt es, das Verhalten von Zonti zu analysieren.
Um die Mengen der Duopolisten voneinander unterscheiden zu können, wird die Produktion von Zonti im folgenden mit $x_Z$ und die von Purelli mit $x_P$ bezeichnet. Für die gesamte Marktnachfrage gilt dann die leicht modifizierte PAF
$$ x_Z + x_P = 5.000 - 20\cdot p \space \space \space \Leftrightarrow\space \space \space p = 250 - 0,05\cdot (x_Z + x_P) \tag{4} $$Die Umsatzfunktion von Zonti ist damit
$$ U_Z = 250x_Z - 0,05\cdot (x_Z + x_P)\cdot x_Z \tag{5} $$und mit der Regel "Grenzumsatz gleich Grenzkosten"
$$ 250 - 0,1x_Z - 0,05x_P = 150 \tag{6} $$findet man die Reaktionsfunktion von Zonti:
$$ x_Z = 1.000 - 0,5x_P \tag{7} $$ Mit der entsprechenden Reaktionsfunktion von Purelli $ x_P = 1.000 - 0,5x_Z $ folgt $$ x_Z = 1.000 - 0,5 \cdot (1.000 - 0,5x_Z) \tag{8} $$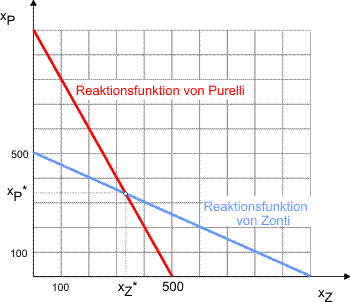
und die von Zonti gewählte Produktionsmenge berechnet sich zu $x_Z = 666,67$ Tsd. Reifen. Da Purelli die gleiche Menge wählen wird, ergibt sich ein Marktangebot von 1.333,33 Tsd. Reifen, so dass der Preis im Vergleich zur Kartelllösung auf 183,33 Euro sinken würde. Der Profit von Zonti würde nun nur noch 22,22 Mio. Euro betragen. Diese Lösung ist insofern stabil, dass keiner der beiden Duopolisten seinen Profit erhöhen könnte, solange der andere an seiner Produktionsentscheidung festhält. Andererseits ist sie aber auch instabil, da sich die beiden Duopolisten durch Absprache in die Kartelllösung verbessern könnten.
Stackelberg-Lösung
Wenn einer der Duopolisten "ahnt", dass sein Konkurrent sich nach Cournot verhalten wird, kann er seine eigene Position verbessern. Angenommen sei, dass Zonti (Marktführer) diese Ahnung besitzt und damit die Reaktionsfunktion Purellis (Marktfolger) in die eigene Entscheidungsfindung einfließen lassen kann. Zonti kann dann analog zu (5), aber unter Verwendung der Reaktionsfunktion von Purelli, den eigenen Umsatz ermitteln
$$ U_Z = 250x_Z - 0,05\cdot (x_Z + [1.000 - 0,5x_Z])\cdot x_Z \tag{9} $$Die Reaktionsfunktion von Purelli erkennt man in Gleichung (9) als Ausdruck in eckigen Klammern. Wiederum unter Verwendung der Regel "Grenzumsatz gleich Grenzkosten" findet man als optimale Angebotsmenge für Zonti die Monopolmenge $x_Z = 1.000$ (= 1 Mio. Reifen). Durch Einsetzen dieses Wertes in die Reaktionsfunktion von Purelli stellt man fest, dass der Marktfolger die halbe Monopolmenge 500 anbietet ($x_P = 500$), so dass das gesamte Angebot auf 1,5 Mio. Reifen steigt und der Reifenpreis auf 175 Euro sinkt. Der Gewinn Zontis betrüge 25, der Purellis 12,5 Mio Euro.
Für den Fall, dass sich beide Duopolisten in der Rolle des Marktführers sähen, betrüge das gesamte Marktangebot 2 Mio. Reifen. In diesem Fall würde der Preis auf 150 fallen und soeben die Kosten decken. Es entstünde eine Situation wie bei vollkommener Konkurrenz, in der die Anbieter nach der Regel "Preis gleich Grenzkosten" handeln. Diese Situation träte hier ein, denn der Preis und die Grenzkosten betragen 150 Euro. Beide Duopolisten befänden sich in einer Nullgewinnsituation.
Bertrand-Lösung
Treten die beiden Duopolisten mit ihrem homogenen Produkt in einen Preiswettbewerb ein, wie es die Verhaltensannahme von Bertrand unterstellt, kann man sich die Preisbildung dynamisch wie folgt vorstellen: Ausgehend von der Kartellsituation wird z.B. Purelli den Preis von 200 auf 190 Euro senken. Da das Produkt nahezu homogen ist, würde Purelli die gesamte Nachfrage auf sich ziehen und Zonti seinen gesamten Absatz verlieren. Darauf kann Zonti nur mit einer Preissenkung reagieren, die mindestens genauso stark ausfällt. In dem eintretenden (unter Umständen ruinösen) Preiskampf würden sich die beiden Anbieter bis auf die Stückkosten (hier gleich den Grenzkosten) herunter konkurrieren und die Lösung entspräche wieder der Situation, die sich auch bei vollkommener Konkurrenz einstellen würde.